INTRODUCCIÓN A LOS PARÁMETROS ESTADÍSTICOS A TRAVÉS DEL DEPORTE

Autor: Diego Alonso Santamaria.

MOTIVACIÓN

Introducir los principales parámetros estadísticos a través del deporte y mostrar una aplicación directa de las matemáticas a la vida real.

INTRODUCCIÓN

Un parámetro de una población es un número que describe su comportamiento general. En poblaciones pequeñas basta con observar los datos para entender su comportamiento, pero en poblaciones grandes esto resulta imposible, y para ello los parámetros nos resumen cómo se distribuyen los datos sin necesidad de estudiarlos uno a uno.

Los parámetros básicos que todo estudiante debe manejar son:

Parámetros de centralización (valores alrededor de los cuales se distribuyen los datos):

• Media: suma de todos los datos dividida entre el número total de datos.
• Mediana: valor que ocupa el lugar central entre del conjunto de datos, cuando están ordenados en forma creciente o decreciente. Si hay un número par de datos, es la media de los dos datos centrales.
• Moda: dato que más veces se repite, es decir, el de mayor frecuencia absoluta.

Parámetros de dispersión:

• Rango: Diferencia entre el valor máximo y mínimo. Da la idea de la dispersión de los datos.
• Desviación Media: promedio de las distancias a la media de los valores de todos los individuos.
• Desviación estándar: medida de dispersión que indica cuánto pueden alejarse los valores respecto a la media. Es útil para buscar probabilidades de que un evento ocurra.
• … (solo usaremos estos en este artículo).

¿Para qué sirven estos parámetros? ¿Son útiles en la vida real para obtener información?

En este artículo se propone un sencillo ejemplo de su aplicación para entender el fútbol, uno de los principales intereses de la juventud actual.

RESUMEN DE LA ACTIVIDAD

CHARLA DIVULGATIVA

Los aficionados de cualquier equipo observan a menudo su clasificación, imaginando con ilusión dónde acabará el equipo, si se salvará del descenso o si harán ruido en Europa. Podemos realizar todas las conjeturas que queramos, pero para sustentar estas ensoñaciones debemos fijarnos en datos objetivos, debemos apoyarnos en la estadística.

A continuación, realizamos un estudio de las últimas 20 temporadas de fútbol. El lector puede tomar sus propias conclusiones viendo las gráficas, pero el uso de parámetros estadísticos nos ayudará a obtener más completa de la competición.

OBJETIVO EUROPA

En el siguiente gráfico podemos ver los puntos del 6º equipo de la Liga, lo cual daba opción directa para jugar competición europea:

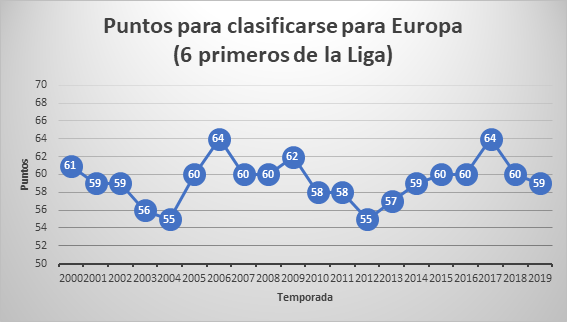
En un simple vistazo, podemos afirmar que para que un equipo se clasifique deberá unos 60 puntos ¿Podemos mejorar esta conclusión? Utilicemos para ello los parámetros estadísticos:

Rango = ValorMáximo – ValorMínimo = 64 – 55 = 9

Idea: gracias al rango sabemos que los puntos necesarios varían en un intervalo de 9 puntos.

Media = 59,3

Mediana = 59,5

Moda = 60

Idea: En la mayoría de ediciones fueron necesarios algo más de 59 puntos. Además, el valor que más veces se han repetido es 60 (nos lo indica la moda).

Desviación media = 1,8

Desviación estándar = 2,4

Idea: la desviación media es el promedio de las distancias a la media de los valores de todos los individuos. Es decir, nos indica que lo normal es que Europa se alcance con 59,3 puntos con un error de ±1,8 puntos.

La desviación estándar nos indica cuánto pueden alejarse los valores respecto a la media.

OBJETIVO EVITAR EL DESCENSO

En el siguiente gráfico podemos ver los puntos del antepenúltimo de la Liga, lo cual obliga a descender de categoría:

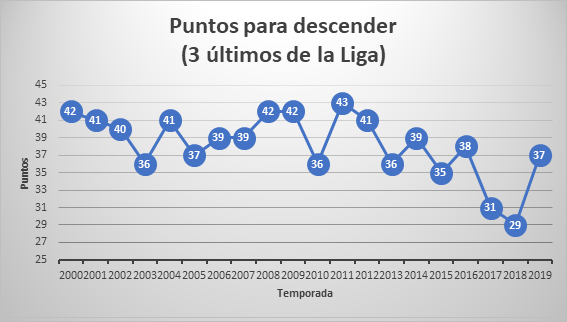
En este ejemplo ya no queda tan claro cuántos puntos son necesarios para no descender, los datos están muy dispersos. Sin embargo, los parámetros estadísticos sí que nos ofrecen la información que a simple vista no somos capaces de obtener (dejamos al lector que interprete los datos):

Rango = ValorMáximo – ValorMínimo = 43 – 29 = 14

Media = 38,2

Mediana = 39

Moda = 36, 39, 41 y 42

Desviación media = 2,9

Desviación estándar = 3,6

Conclusiones:

Cuando observamos la segunda gráfica observamos que los datos eran “más dispersos” y no fuimos capaces de obtener ninguna información de ello. Si comparamos los parámetros de ambas gráficas, las desviaciones de la segunda son mucho mayores. Esto nos confirma la dispersión que intuíamos con datos objetivos.

Además, gracias a los parámetros podemos percatarnos de que los datos se encuentran en torno a los valores de centralización (información que no éramos capaces de extraer observando la nube de datos).

Este ha sido un ejemplo introductorio a los parámetros estadísticos. Ha sido un ejemplo pequeño, en el que podríamos haber obtenido la información deseada utilizando una calculadora y varios minutos de nuestro tiempo. Sin embargo, en la vida real se trabaja con grandes nubes de datos y sin la ayuda de los ordenadores seríamos incapaces de obtener conclusiones de ello. Para esto sirven los parámetros, para resumir e interpretar nubes de datos que de otra forma serían imposibles de abarcar.

ESCRITO POR …

Diego Alonso Santamaría, profesor de matemáticas, divulgador y periodista deportivo.

Mail de contacto: elmatematicoquequisoserpivot@gmail.com